이미지 변환(Image Transformations) 종류와 호모그래피 (Homography)

1. 이미지 변환 : Image Transformations

이미지의 변환이란 각 이미지 픽셀의 좌표 (x,y)를 다른 좌표 (x',y')로 매핑하는 것을 말합니다.

변환의 종류에는 변환 후 기존의 특성을 어느정도 보존하는가에 따라 크게 강체 변환, 유사 변환, 선형 변환, 아핀 변환, 투영 변환으로 나눌 수 있습니다.

 

 

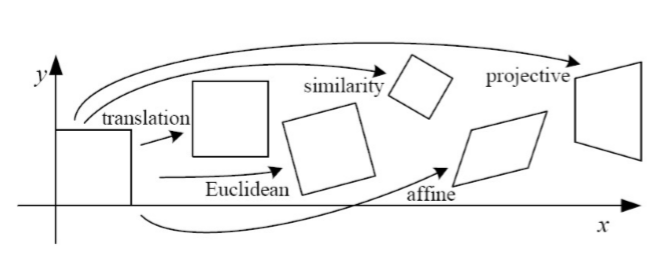
2. 변환 종류

- 강체 변환 (Rigid-Body Transformation)

 

물체의 평행 이동(Translation), 회전(Rotation) 등 물체의 위치와 방향만 바꾸고 형태가 변하지 않는 (강체) 변환을 말합니다.

3자유도를 가지며, 각 변환에 대한 매핑 함수는 다음과 같습니다.

 

$$이동 변환 (Translation) : \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} x \\ y\end{bmatrix} + \begin{bmatrix} T_x \\ T_y \end{bmatrix} \rightarrow \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & 0 & T_x \\ 0 & 1 & T_y \end{bmatrix} \begin{bmatrix} x \\ y \\ 1\end{bmatrix}$$

 

$$회전 변환 (Rotation) : \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\begin{bmatrix} x \\ y\end{bmatrix}$$

 

이때 회전 변환은 물체 자체가 회전하는 것이 아니라, 물체가 속한 좌표계의 원점 (0, 0)을 기준으로 좌표계가 회전하는 것 입니다. 따라서 두 좌표의 원점간 거리가 다르다면 두 좌표간의 관계를 회전변환만으로 표현할 수 없습니다. 이를 해결하기 위해서는 두 좌표의 원점간 거리 (Scale)을 고려한 매핑 함수를 사용하고 Scale 변화 값을 1로 계산하여 두 좌표간 회전각을 구할 수 있습니다.

 

$$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} S\cos\theta & -S\sin\theta \\ S\sin\theta & S\cos\theta \end{bmatrix}\begin{bmatrix} x \\ y\end{bmatrix}$$

 

위 식을 다시 정리하면, 

$$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} x & -y \\ y & x \end{bmatrix}\begin{bmatrix} S\cos\theta \\ S\sin\theta\end{bmatrix}$$

 

위 식을 계산하고, Scale 변화 값을 1로 하여 두 좌표간의 회전각 관계를 계산할 수 있습니다.

 

위의 평행이동과 회전 변환을 모두 고려한 매핑 함수는 다음과 같이 표현할 수 있습니다.

{$a = S\cos\theta, b = S\sin\theta$)

$$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & -b \\ b & a \end{bmatrix}\begin{bmatrix} x \\ y\end{bmatrix} +\begin{bmatrix} c \\ d\end{bmatrix}$$

위 행렬식을 전개하면, $ x' = ax-by+c, y' = bx+ay+d $ 이며, 이를 다시 행렬식으로 표현하면 다음과 같습니다.

 

$$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} x & -y & 1 & 0 \\ y & x & 0 & 1 \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ d \end{bmatrix} $$

 

- 유사 변환 (Similarity Transformation)

 

물체의 이동, 회전을 포함하여 물체의 크기(Scale)가 달라질 수 있는 변환을 말합니다.

4자유도를 가지기 떄문에 두 쌍의 좌표가 있으면 유일한 변환 관계를 정의할 수 있으며, 크기 변환에 대한 매핑 함수는 다음과 같습니다.

 

$$크기 변환 (Scale) :\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} S_x & 0 \\ 0 & S_y \end{bmatrix}\begin{bmatrix} x \\ y\end{bmatrix}$$

 

 

- 선형 변환 (Linear Transformation)

 

벡터 공간 간의 변환 ($f : V \rightarrow W $)으로 임의의 $a\in F, u, v,\in V$ 에 대해, $f(au + v) = af(u) + f(v)$ 의 조건을 만족하는 변환입니다.

즉, 벡터의 위치는 변하지 않고, 방향과 크기만 변하는 변환을 말합니다.

회전 변환, 크기 변환, 반전 변환, 전단 변환 등이 속하며, 전단 변환의 매핑 함수는 다음과 같습니다.

 

$$전단변환 (Shear) :\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & a_x \\ a_y & 1 \end{bmatrix}\begin{bmatrix} x \\ y\end{bmatrix} $$

 

 

- 아핀 변환 (Affine Transformations)

선형 변환과 이동 변환을 모두 포함하며 공간의 평행성을 보존하는 변환을 아핀 변환이라고 합니다.

우측의 잎사귀가 반복되는 프랙탈 이미지가 대표적인 아핀 변환인데, 잎사귀는 각 작은 잎사귀의 평행 이동 변환, 회전 변환, 크기 변환의 조합에 의해 구성되어 있습니다.

 

자유도는 6으로, 3쌍의 좌표가 있으면 변환 관계를 유일하게 정의할 수 있으며, 아핀 변환의 매핑 함수는 다음과 같습니다.

 

$$아핀 변환 (Affine) :\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} x \\ y\end{bmatrix} + \begin{bmatrix} e \\ f \end{bmatrix}$$

$$\rightarrow \begin{bmatrix} x' \\ y' \\1 \end{bmatrix} = \begin{bmatrix} a & b & e\\ c & d & f \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix} x \\ y \\ 1\end{bmatrix}$$

 

 

- 투영 변환 (Projective Transformation)

 

원근 변환 혹은 호모그래피(Homograpy)라고도 하며, 3D 공간에서 2D공간으로 투영하거나, 서로 다른 두 평면 간의 매핑 관계를 모델링하기 위한 변환입니다.

우리의 두 눈은 물체의 서로 다른 평면을 보고 있으며, 이로 인해 평행성이 깨지고 물체에 원근감이 생기게 됩니다. 우리에게서 멀어질수록 물체가 한 점으로 모이게 되는 것처럼 보이는 것이 바로 이 투영 변환과 같은 원리입니다.

 

호모그래피는 8자유도를 가지며, 4쌍의 좌표를 통해 변환 관계를 정의할 수 있습니다.

호모그래피가 9자유도가 아닌 8자유도를 가지는 이유는 동차 좌표계(Homogeneous Coordinates)에서 정의되어 9개의 Factor 중 Scale Factor 값을 무시해도 되기 때문입니다.

 

여기서 동차 좌표계란, 3차원의 한 좌표를 특정 방향으로의 2차원 평면으로 투영할때 동일한 방향으로 무한대 거리에 있는 평면들을 표현할 수 있는 좌표계입니다. (즉, 원근에 따라 물체의 투영비율 조절이 가능하게 됩니다.)

동차 좌표계는 유클리디안 좌표 (x, y)를 scale factor인 w를 추가하여 (x, y, w)로 표현할 수 있으며, 원래의 유클리디안 좌표계로 다시 나타내려면 (x/w, y/w, 1)과 같이 scale 값을 나눠주면서 표현할 수 있습니다.

만약 유클리디안 좌표계로 바꾼 scale 값이 1이라면 원래 물체의 좌표와 동일한 위치임을 나타내며, scale 값이 0이면 동치좌표계의 scale이 무한대임을 알 수 있습니다. ($1/\infty = 0$)

 

 

호모그래피를 이용한 이미지 파노라마

 

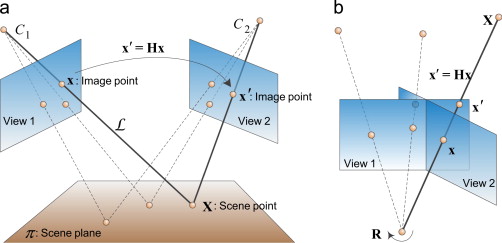
위에서 우리는 왼쪽 평면과 오른쪽 평면에 투영된 물체의 위치가 거리가 변해도 같은 점을 나타내고 있음을 확인할 수 있습니다. 이러한 관계를 호모그래피로 표현할 수 있습니다.

 

호모그래피 함수는 아래와 같이 표현됩니다.

 

$$투영 변환 (Projective) : w \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\h_{31} & h_{32} & h_{33}\end{bmatrix}\begin{bmatrix} x \\ y \\ 1\end{bmatrix}$$

 

위 식을 DLT (Direct Linear Transformation) 방법을 이용해 다음과 같이 변형할 수 있습니다.

 

$$\begin{bmatrix} x & y & 1 & 0 & 0 & 0 & -x'x & -x'y & -x' \\ 0 & 0 & 0 & x & y & 1 & -y'x & -y'y & -y' \end{bmatrix}\begin{bmatrix} h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \\ h_{33} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}$$

$$\rightarrow minimize \parallel Ah - 0 \parallel ^2$$

 

따라서 Homography 함수는 좌표 성분 A에 대해 $A^TA$의 가장 작은 eigenvalue를 가지는 eigenvector가 됩니다.