[차원 축소] 차원 축소 개요

1. 차원

 

1.1 차원이란?

 

기하학적으로 차원은 공간 내에 있는 점의 위치를 나타내기 위해 필요한 축의 개수를 말합니다.

예를 들어 2차원 공간의 점은 두 개의 축 (x, y) 으로, 3차원 공간의 점은 세 개의 축 (x, y, z) 으로 표현이 가능하죠.
즉, 어떤 데이터(점)의 특징(위치)을 서술하는데 사용되는 독립적인 특성(차원)의 개수, 정보량이라고 생각할 수 있습니다.

따라서 차원의 크기가 커질 수록 데이터를 해석할 수 있는 정보를 더 많이 가지고 있다고 생각할 수 있습니다.

 

0차원 점, 1차원 선분, 2차원 사각형, 3차원 정육면체와 4차원 초입방체

 

이러한 차원의 의미를 일상 생활의 데이터에 적용해볼까요?

이미지의 경우 이미지를 구성하는 각각의 픽셀들이 이미지를 나타내는 독립적인 특성들이 될 것 입니다.

따라서 이미지 전체의 픽셀 개수가 차원의 크기에 해당되며, 100x100 크기 이미지의 차원의 개수는 10,000개, 1000x1000 크기 이미지의 차원의 개수는 1,000,000 개가 됩니다.

 

그렇다면 동일한 이미지에서 차원 크기의 무엇을 의미할까요?

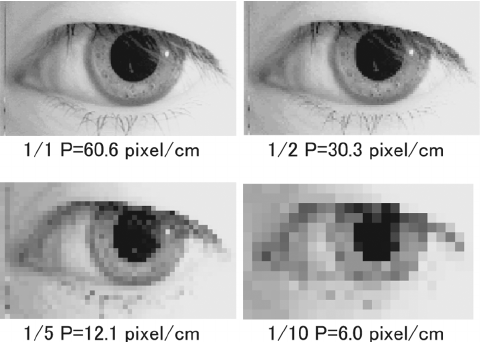
아래의 이미지를 보면 픽셀이 많아질수록 눈의 더 디테일한 형태까지 표현할 수 있는 것을 확인할 수 있습니다.

하지만 우리가 필요한 정보가 단순히 눈 인지, 아닌지를 구분하는 것 이라면, 적은 픽셀 개수(데이터량)로도 눈의 여부를 결정할 수 있을 것 입니다.

 

 

이처럼 우리는 차원을 축소하거나 확장해 여러 문제들을 해결할 수 있으며, 주로 문제를 단순화 하기 위한 방법으로 차원을 축소하거나 확장하는 방법을 사용합니다.

 

차원 축소 및 확장을 통한 문제의 단순화

 

이번 포스팅에서는 차원을 축소하는 방법에 대해 정리해 보겠습니다.

 

 

1.2 차원의 저주

 

흔히 데이터의 차원과 관련된 문제에서 흔히 등장하는 차원의 저주라는 용어가 있습니다.
이는 데이터의 차원이 증가할 수록 데이터를 담고 있는 공간의 부피가 기하급수적으로 증가하면서 데이터 밀도가 희박해지는 현상을 말합니다.

 

차원 증가에 따른 데이터 밀도

 

데이터 밀도가 희박하다는 얘기는 각 데이터 간 거리가 늘어난다는 얘기인데요,
데이터 분석 (예측) 시 데이터 간 거리가 늘어날 수록 우리는 더 많은 extrapolation을 해야합니다. 즉, 불확실성이 높아지게 됩니다.

 

따라서 데이터 개수가 일정할 때 차원의 수가 증가할수록 데이터 예측 성능은 점점 감소하며, 차원의 수가 데이터 개수보다 커지게 되면 (이러한 경우를 underdetermined 문제라고 볼 수 있습니다.) 성능은 급격히 떨어지게 됩니다.

 

차원 수 증가에 따른 회기 분석 결과 (N data = 10)

 

차원 수 증가에 따른 분류기 성능

 

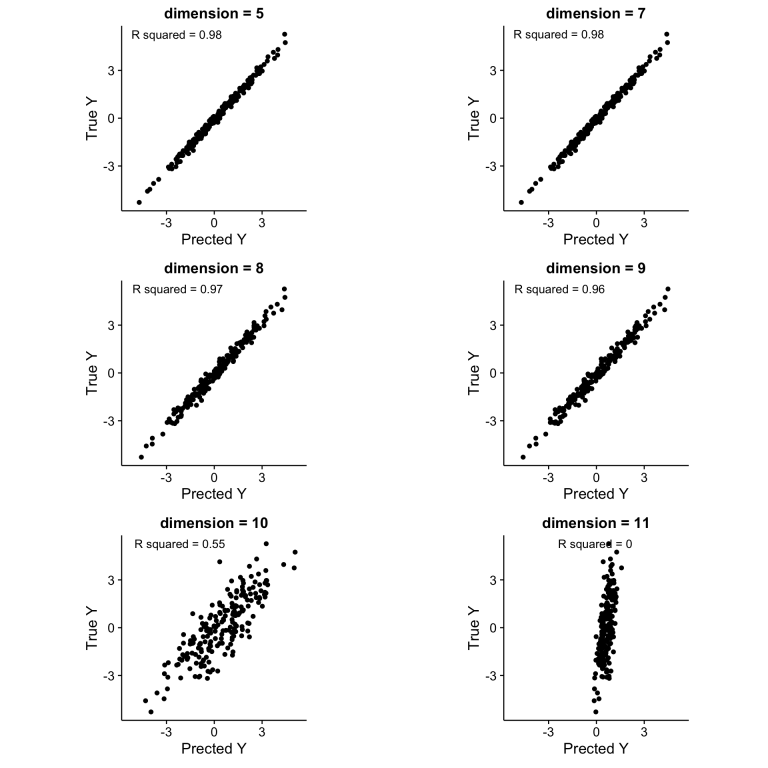
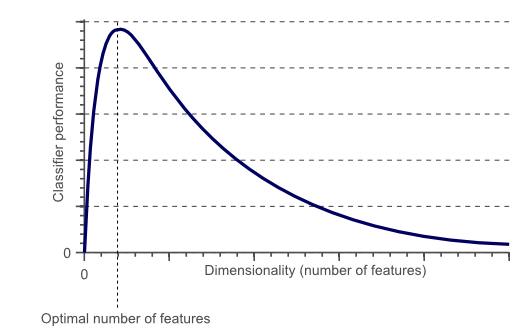
이를 해결하기 위한 가장 간단한 방법은 데이터의 밀도를 높이기 위해 많은 데이터를 집어넣는 것 입니다.

하지만 현실적으로 이를 만족하기 위한 데이터를 모으기 위해서는 어마어마한 비용의 리소스들을 고려해야됩니다.

따라서 우리는 리소스가 많이 드는 데이터 추가 방법보다 차원의 수를 줄이는 방법을 생각해야 합니다.

 

2. 차원 축소 방법

 

2.1 투영 (Projection)

 

우리는 데이터가 공간 상에 균일하게 퍼져있기를 바라지만, 실제로는 그렇지 않은 경우가 대부분 입니다.

많은 특성들이 아무 의미 없는 노이즈 성분이거나, 거의 변화가 없을 수 있고, 서로 강하게 연관된 특성들이 있을 수도 있습니다.

결과적으로는 고차원 공간 상의 데이터들은 저차원의 부분 공간 (subplace)과 가까이에 분포되어 있습니다.

 

부분 공간(Z) 으로의 데이터 투영

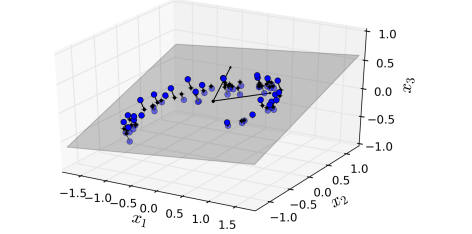
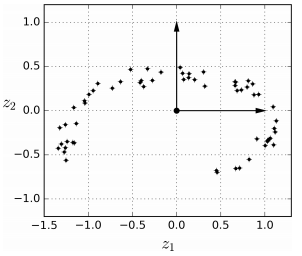
이처럼 고차원 공간 상의 데이터를 저차원의 부분 공간으로 투영하는 방법으로 주성분 분석 (PCA) 방법이 대표적입니다.

 

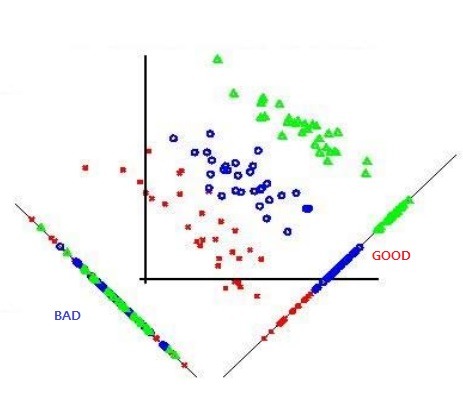
그러나 아래와 같이 데이터의 부분 공간이 꼬여있거나 뒤틀린 경우, 투영으로 정확한 데이터 분포의 특성을 정의할 수 없게 됩니다.

 

3D Swiss Roll 형태의 데이터 분포를 펼친 2D 매니폴드 평면

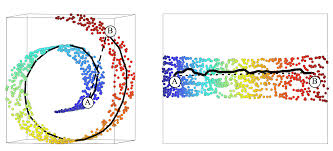
이때 꼬여있는 방향대로 부분 공간을 펼칠 수 있다면 투영과 같이 데이터를 특정 평면상에 분포시킬 수 있습니다. 

단, 이를 위해서는 데이터 분포가 매니폴드 가정 (고차원의 데이터 집합은 저차원의 매니폴드 상에 위치할 수 있다는)을 만족해야 합니다.

 

2.2 매니폴드 학습 (Manifold Learning)

원은 모든 점에서 국소적으로 직선과 같은 구조를 갖고 있다.

매니폴드란 위상수학에서 국소 유클리드 공간과 닮은 위상 공간(다양체)을 의미합니다. 즉, 유클리드 공간에서 같은 모양을 갖고 있으나, 전체 공간상에서 봤을 때는 독특한 구조를 갖고 있는 것을 의미합니다.

 

예를 들어, 원은 모든 점에 대해 국소적인 유클리드 공간에 투영 했을때, 직선과 같은 동일한 구조를 갖고 있습니다. (원은 1차원 다양체)

매니폴드 가정에 따르면 2차원인 원은 1차원인 직선을 매니폴드로 갖고 있으며, 1차원의 직선을 뒤틀어서 2차원의 원을 만들 수 있습니다.

 

위의 Swiss Roll 그림을 다시 보면, 고차원에서 데이터 A와 B간 가장 가까운 유클리디안 거리상에서 의미상으로는 (데이터간 밀도가 낮아짐) 가깝지 않을 수 있으나, 이를 매니폴드 평면에 놓고 봤을 땐 의미상으로 더 가까운 것을 알 수 있습니다.

 

매니폴드 학습이란 아래 그림과 같이 고차원의 꼬여있는 데이터 분포에서 매니폴드(실선)를 모델링하는 것을 말합니다.

 

 

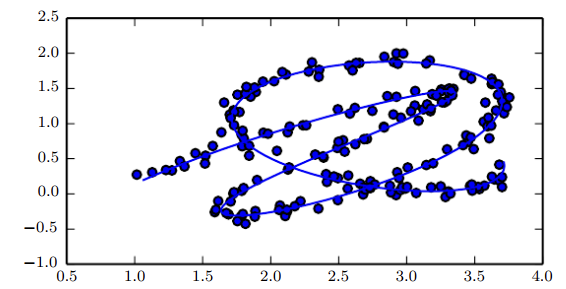
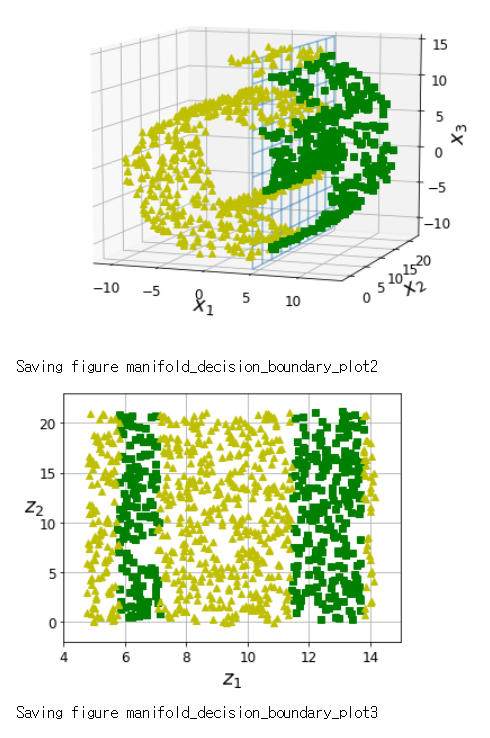
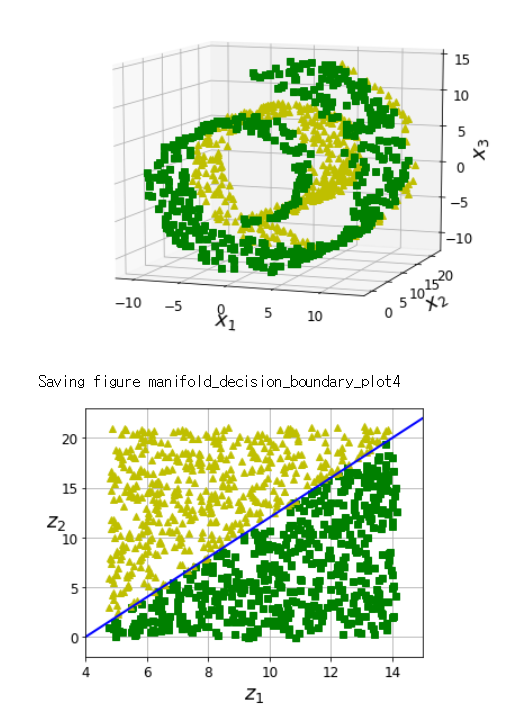
물론 모든 경우에서 매니폴드가 데이터 분포를 더 잘 표현하는 것은 아닙니다.

아래와 같이 고차원 평면에서의 결정 경계가 데이터를 더 잘 표현할 수도 있습니다.

따라서 데이터 분포 특성을 잘 확인하여 해당 특성에 맞는 차원 축소 방법을 사용해야 합니다.

 

매니폴드 모델이 적합하지 않은 데이터 분포와 적합한 데이터 분포.  좌측의 Swiss Roll 데이터 분포는 매니폴드 평면보다 X1=5 평면에서 데이터를 더 잘 구분할 수 있다.

 

다음 포스팅에서는 차원 축소 알고리즘 중 하나인 주성분 분석 : PCA (Principle Component Analysis)에 대해 알아보겠습니다.

 

참고 도서 :

Hands-On Machine Learning with Scikit-Learn & TensorFlow, 한빛미디어