1. Python을 이용한 PCA
1.1 Iris DataSet
Iris DataSet을 이용해 PCA를 실행해 보겠습니다.
Iris DataSet은 150개의 Iris 꽃 개체 대한 데이터로 구성되어있으며 사이킷런을 이용해 손쉽게 불러올 수 있습니다.
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
Iris = load_iris()
iris_df = pd.DataFrame(data = np.c_[Iris['data'], Iris['target']], columns=Iris['feature_names']+['target'])
iris_df['target'] = iris_df['target'].map({0:"setosa", 1:"versicolor", 2:"virginica"})
X = iris_df.iloc[:, :-1]
Y = iris_df.iloc[:,[-1]]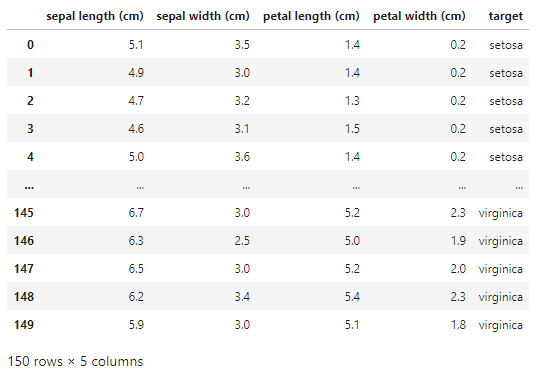
1.2 SVD
위의 Iris Data 중 Sepal과 Petal 데이터를 X, Target을 Y로 설정하여 X에 따라 Y를 구분할 수 있는지 확인해보고자 합니다. 이때, PCA는 데이터 셋의 평균이 0이라고 가정하기 때문에, 데이터를 원점을 기준으로 분포하도록 전처리 과정이 필요합니다.
이후 Numpy의 특이값 분해 함수인 svd()를 통해 주성분들을 구합니다.
X_centered = X - X.mean(axis=0) # Data Centering (Standardization)
U, S, V_T = np.linalg.svd(X_centered) # Cov = U Sigma V^T
V = V_T.T[:, :] # EigneVectors

Iris Data의 특성 수가 총 4개이므로 차원 수는 총 4개이며, Eignevector(주성분)의 개수 또한 4개가 됩니다.
1.3 d차원으로 투영
위에서 추출한 주성분들에 대해 각 차원으로 데이터 X를 투영하여 차원 축소를 수행할 수 있습니다.
투영은 데이터를 특정 축으로 선형변환(내적)하는 것이므로 $(Z = X \centerdot V_d)$ 아래와 같이 구할 수 있습니다.
Z = X_centered.dot(V)
위에서 나온 주성분 축 1과 2를 축으로 하는 평면으로 데이터를 투영한 결과와, 주성분 각 축 (1, 2, 3, 4)로 투영한 결과는 아래와 같습니다.
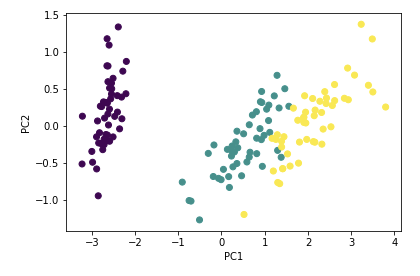




위에서 보듯이 주성분 1차 축에서 데이터의 분산이 제일 크며, 정보를 제일 잘 표현하고 있다는 것을 확인할 수 있습니다.
2. 사이킷런을 이용한 PCA
2.1 사이킷런을 이용한 PCA
사이킷런 또한 특이값 분해 (SVD)를 이용하여 데이터의 주성분을 계산합니다.
이때 사이킷런의 PCA모델은 데이터의 Standardization을 자동으로 수행합니다.
from sklearn.decomposition import PCA
pca = PCA(n_components = 4)
#n_components : 투영할 차원 수, 0.0~1.0 사이로 값을 설정 시 해당 분산의 비율이 필요한 차원 수로 설정됨
Z = pca.fit_transform(X)
이후 pca.components_ 변수를 통해 주성분을 확인할 수 있습니다.
2.2 설명된 분산 비율
pca.explained_variance_ 및 pca.explained_variance_ratio_ 변수를 통해 각 주성분 축으로 투영된 데이터들의 분산값(공분산 행렬의 고유값)과 그 비율을 확인할 수 있습니다.

위의 수치를 보시면, 1차 주성분 축에 데이터셋 분산의 약 92%가 놓여져 있고, 그 다음 주성분 축으로 갈수록 데이터의 분포 양이 줄어듬을 확인할 수 있습니다.
'개발 공부 > ML&DL' 카테고리의 다른 글
| [최적화] 가중치 규제 L1, L2 Regularization의 의미, 차이점 (Lasso, Ridge) (3) | 2022.06.05 |
|---|---|
| [차원 축소] Kernel-PCA (0) | 2020.03.02 |
| [차원 축소] 주성분 분석 (PCA, Principal Component Analysis) (0) | 2020.02.09 |
| [차원 축소] 차원 축소 개요 (1) | 2020.01.27 |




댓글