1. 수학적 최적화(Optimization)와 과적합 (Overfitting)
수학에서 최적화란, 특정 집합에 대한 목적 함수(Objective Function)를 최소화 혹은 최대화시키는 최적해 (파라미터)를 찾는 것을 말합니다.
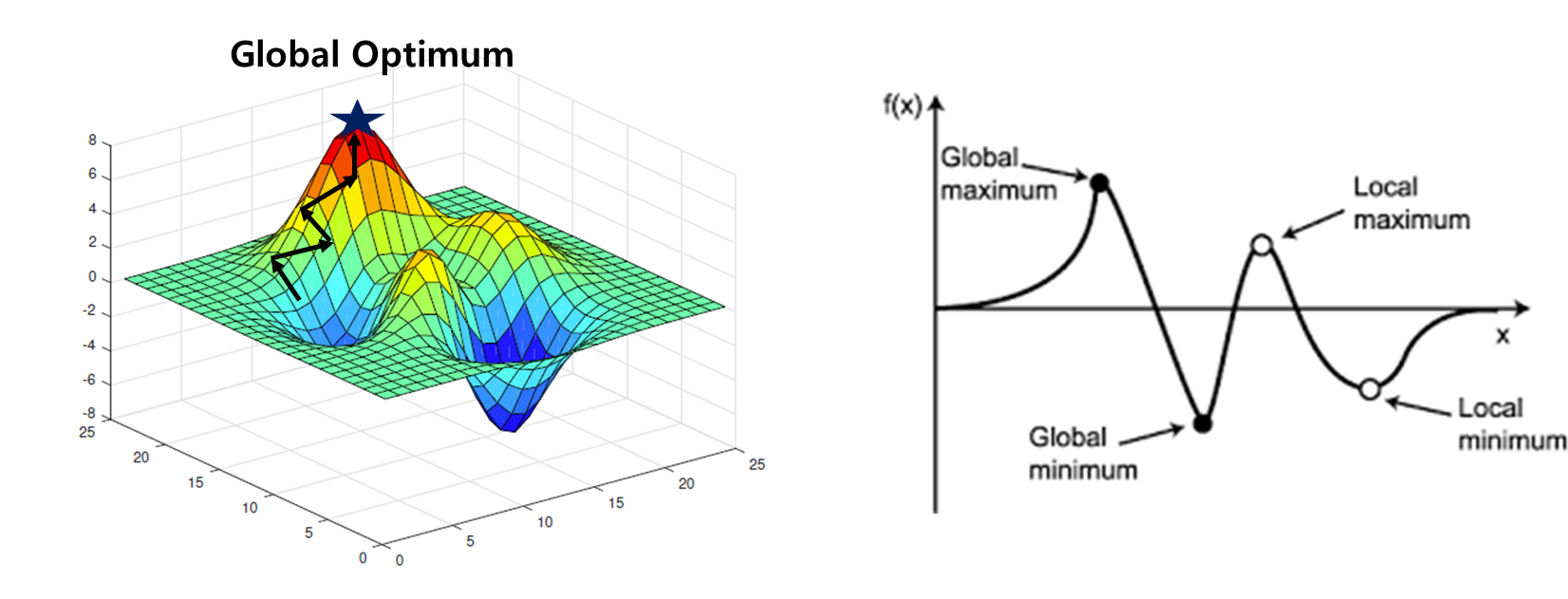
머신러닝 및 딥러닝 알고리즘은 모두 어떤 현상을 가장 잘 설명하기 위한 모델 함수를 찾는 방법입니다.
모델을 찾을 때, 모델의 예측 결과와 실제 결과 간 오차가 발생하게 되고 이를 표현한 함수를 손실 함수(Loss Function, Cost Function)이라고 합니다. 학습 기반의 머신러닝 및 딥러닝 알고리즘은 모델 성능을 높이기 위해 이 손실 함수를 최소화할 수 있는 방향으로 학습을 진행하게 됩니다.
즉, 손실 함수의 최적화 문제라고 볼 수 있습니다.

우리는 모델을 만들 때, 대부분 한정된 일부 데이터 만을 학습 데이터로 사용하게 됩니다.
그러다 보니 학습 데이터에만 존재하는 특징(노이즈)들이 과하게 모델에 반영되어 손실 함수가 필요 이상으로 작아지게 되는 경우가 발생합니다.
이를 과적합 혹은 오버피팅 (Overfitting)이라고 합니다.
오버피팅이 발생하면 모델이 학습에 사용된 데이터만 잘 설명하고 데이터의 일반적인 특징을 반영하지 못해 좋은 모델이라고 할 수 없습니다.
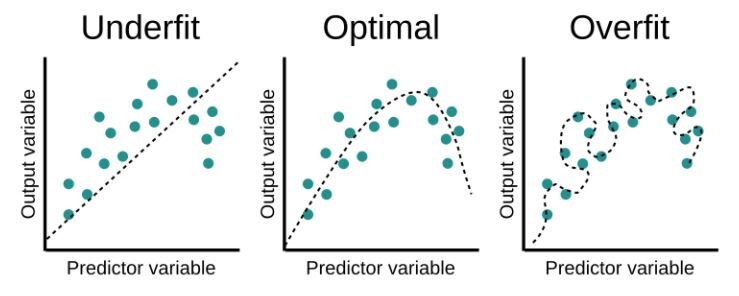
오버피팅 문제를 해결하기 위한 방법으로는 아래 방법들이 있습니다.
- 학습 데이터 양을 늘리기
- 배치정규화 (Batch Normalization)
- 모델의 복잡도 줄이기
- 드롭아웃 (Drop-Out)
- 가중치 규제 (Weight Regularization)
이중 가중치 규제란 모델의 손실 함수값이 너무 작아지지 않도록 특정한 값(함수)를 추가하는 방법입니다.
이를 통해 특정한 weight 값이 과도하게 커져서 일부 특징에 의존하는 현상을 방지하고 데이터의 일반적인 특징 (일반화, Generalization)을 잘 반영할 수 있도록 해줍니다.
가중치 규제에는 L1 규제 (L1 정규화, L1 Regularization, Lasso), L2 규제 (L2 정규화, L2 Regularization, Ridge)가 있습니다.
2. L1 norm, L2 norm, Lp norm
L1 Regularization과 L2 Regularization은 모델의 손실 함수(Loss Function, Cost Function)에 각각 L1 Loss Function, L2 Loss Function을 추가해 준 것을 말합니다.
Norm은 유한 차원의 벡터 공간에서 벡터의 절대적인 크기(Magnitude)를 혹은 벡터간 거리를 나타냅니다.
Norm은 특정한 속성을 만족하며, 측정 가능한 기능의 공간인 Lp 공간 (Lp Space) 혹은 르베그 공간 (Lebesgue Space)에서의 norm을 Lp norm (혹은 p-norm) 이라고 합니다.
Lp norm을 수식화 하면 다음과 같습니다.
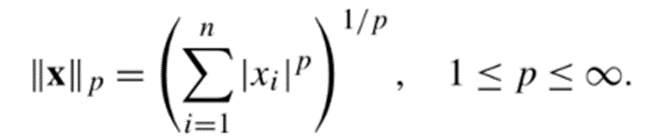
위 수식에서 n과 p는 실수이며, p는 norm의 차수, n은 벡터의 차원 수를 나타냅니다.
p의 차수에 따라서 Lp norm은 아래와 같은 형태를 띄게 됩니다.
2차원 벡터 공간에서 L1 norm의 분포는 마름모꼴을, L2 norm은 원을 나타내고 있으며, p가 무한대로 갈수록 정사각형의 형태를 띄게 됩니다.
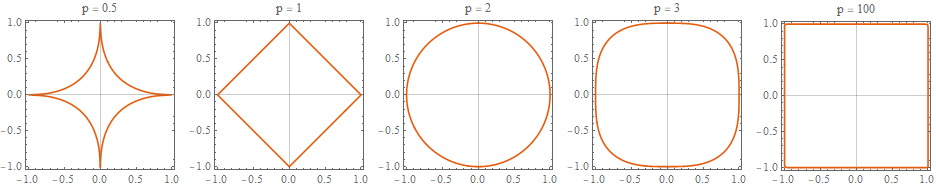
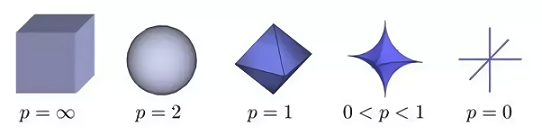
위의 형태의 특수성에서 보는 것 처럼, p가 1, 2, ∞ 일때의 norm인 L1 norm, L2 norm, L∞ norm을 많이 사용합니다.
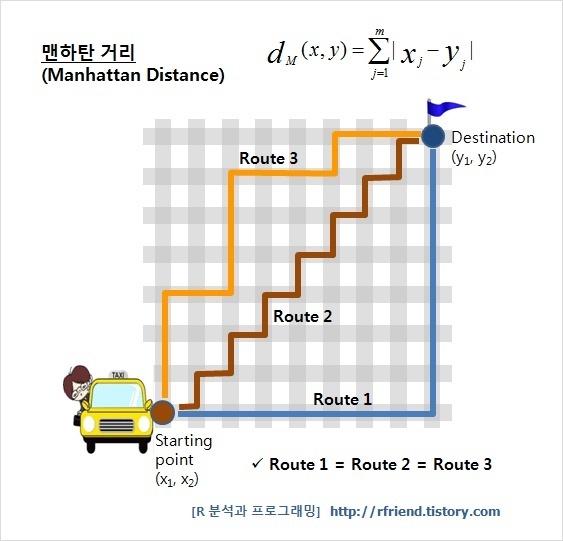
- L1 norm (Manhattan distance, Taxicab geometry), p = 1
- L1 norm은 맨하탄 거리 혹은 택시 거리라고 많이 알려져 있으며, 택시가 도시의 블록 사이를 이동해 다른 지점으로 이동하는 것과 같이 표현하고 있습니다.
- 특정 방향으로만 움직일 수 있는 조건이 있는 경우, 두 벡터 간의 최단 거리를 찾는데 사용되는 방법입니다.
- L1 loss는 아래 수식과 같이 실제 값과 예측 값 오차들의 절대값들에 대한 합을 나타냅니다.
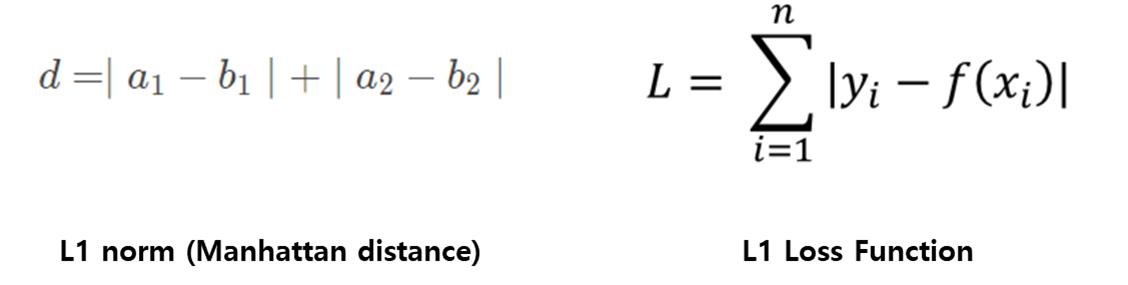
- L2 norm (Euclidean distance), p = 2
- L2 norm은 유클리드 거리라고도 하며, 두 점 사이의 최단 거리를 측정할 때 사용됩니다.
- L2 loss는 실제 값과 예측 값 오차들의 제곱의 합으로 나타냅니다.
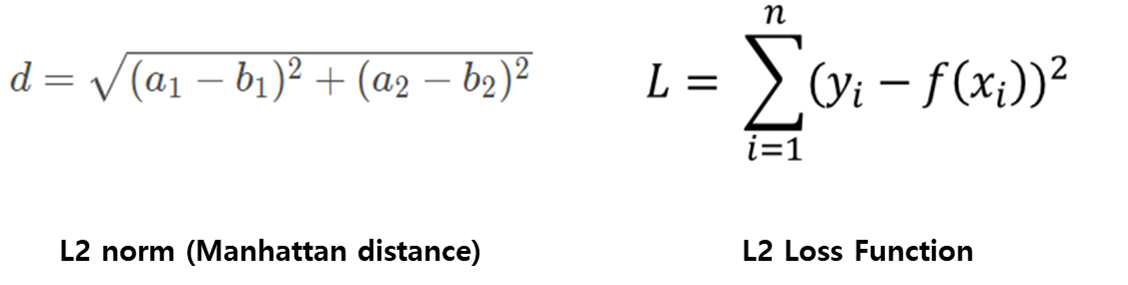
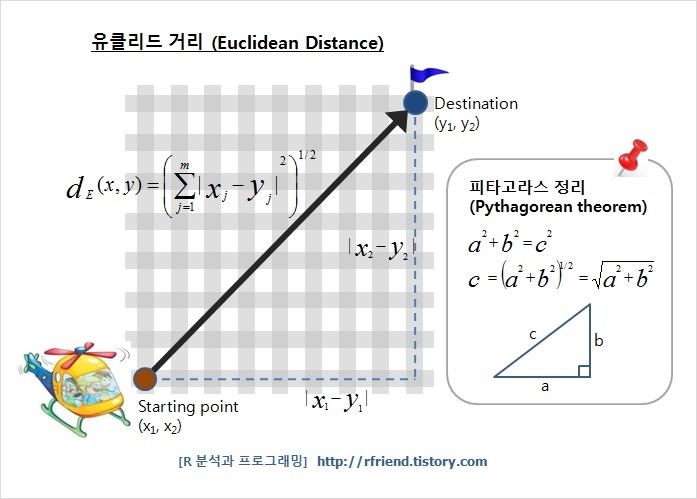
L1과 L2 norm의 수식과 기하학적 특징에서 그 차이를 비교해보면, L1 norm은 다른 점으로 이동하는데에 다양한 방법이 있는 반면에 L2 norm은 단 한 가지의 방법만 있으며, L2 norm은 수식에서 오차의 제곱을 하기 때문에 outlier에 대해 더 큰 영향을 받습니다.
따라서 L1 norm은 다른 점으로 이동하는 다양한 방법 (feature, weight) 중 특정 방법을 0으로 처리하는 것이 가능하여 중요한 가중치만 남길 수 있는 feature selection이 가능하며, 오차의 절대값을 사용하기 때문에 L2 대비 outlier에 좀 더 robust 합니다.
그러나 0에서 미분이 불가능해 Gradient-Based Learning 시 사용에 주의가 필요하고, 편미분 시 weight의 부호만 남기 때문에 weight의 크기에 따라 규제의 크기가 변하지 않으므로 Regularization 효과가 L2 대비 떨어집니다.
L2 norm은 오차의 제곱을 사용하기 때문에 outlier에 대해 L1 보다 더 민감하게 작용합니다.
따라서 weight의 부호 뿐만 아니라 그 크기만큼 페널티를 줄 수 있어 특정 weight가 너무 커지는 것을 방지하는 weight decay가 가능해집니다.
이러한 특징 때문에 L2 norm이 weight에 대한 규제에 좀 더 효과적이고 일반적으로 학습 시 더 좋은 결과를 얻을 수 있어 L1 norm보다 많이 사용되어집니다.
3. L1 Regularization (Lasso), L2 Regularization (Ridge)
위에서 설명한 것 처럼 Regularization은 학습 기반의 알고리즘에서 모델이 과적합되지 않도록 손실 함수에 특정한 규제 함수를 더하여 손실 함수가 너무 작아지지 않도록 weight에 페널티를 주는 기법입니다.
더해지는 규제 함수에 따라 L1 Regularization (Lasso), L2 Regularization (Ridge) 등이 있으며, 이를 더한 모델의 Cost Function은 아래와 같습니다.

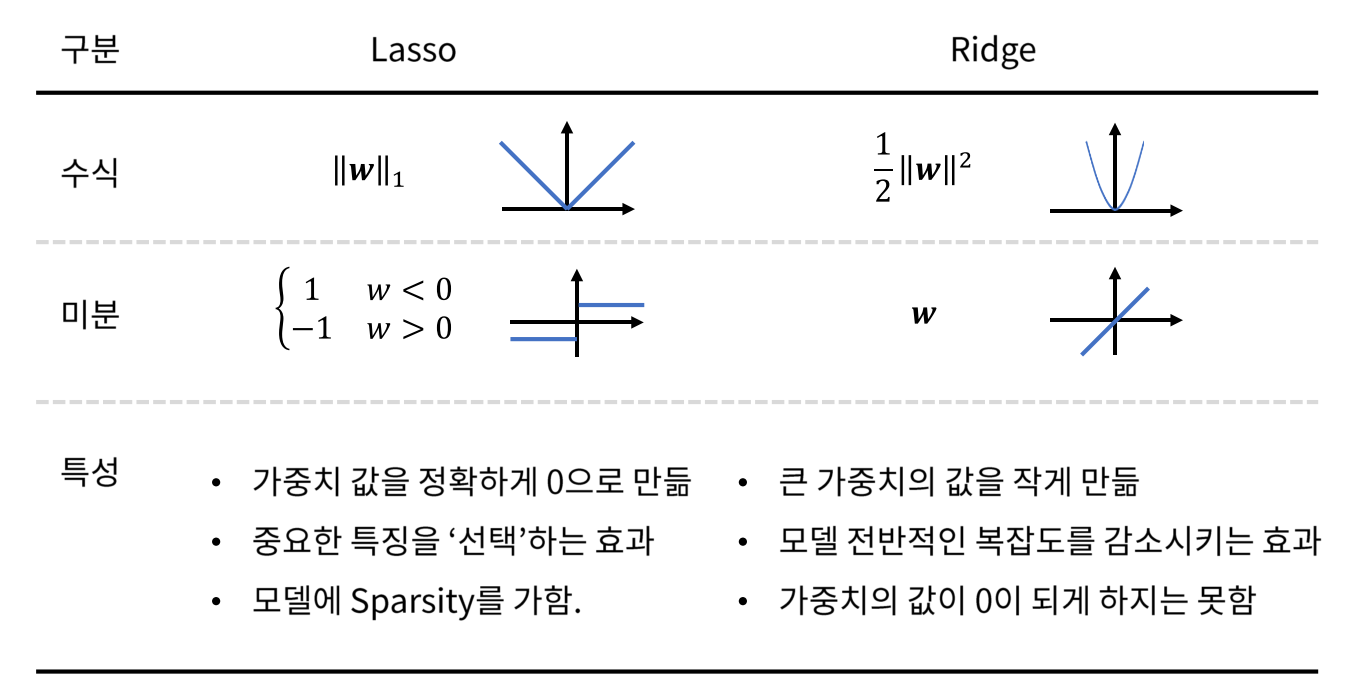
L1 Regularization (Lasso)은 기존 Cost Function에 가중치의 절대값의 합을 더하는 형태로, 미분 시 weight의 크기에 상관 없이 부호에 따라 일정한 상수값을 빼거나 더해주게 됩니다.
따라서 특정 weight들을 0으로 만들 수 있어 원하는 weight만 남길 수 있는 feature selection 역할을 할 수 있습니다.
이를 통해 특정 가중치를 삭제해 모델의 복잡도를 낮출 수 있습니다.
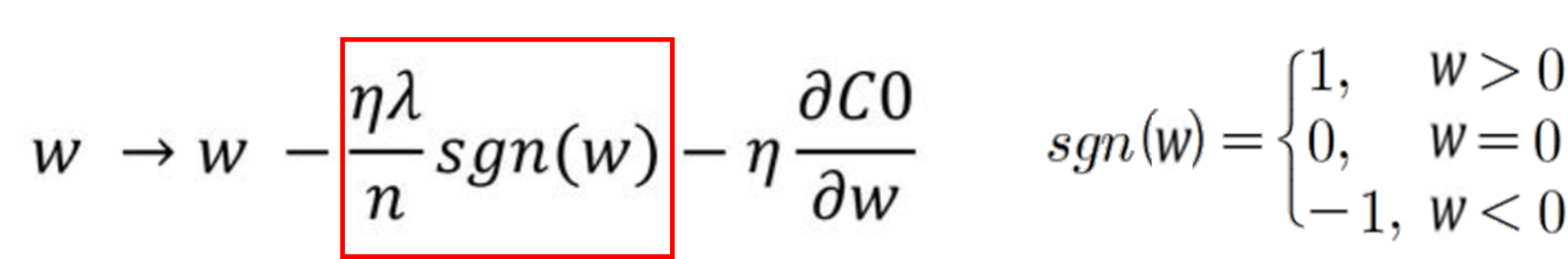
L2 Regularization (Ridge)은 기존 Cost Function에 가중치 제곱의 합을 더하는 형태로, weight의 크기에 따라 weight 값이 큰 값을 더 빠르게 감소시키는 wieght decay 기법입니다.
weight의 크기에 따라 가중치의 패널티 정도가 달라지기 때문에 가중치가 전반적으로 작아져서 학습 효과가 L1 대비 더 좋게 나타납니다.
λ(람다) 값에 따라 패널티의 정도를 조절할 수 있습니다.
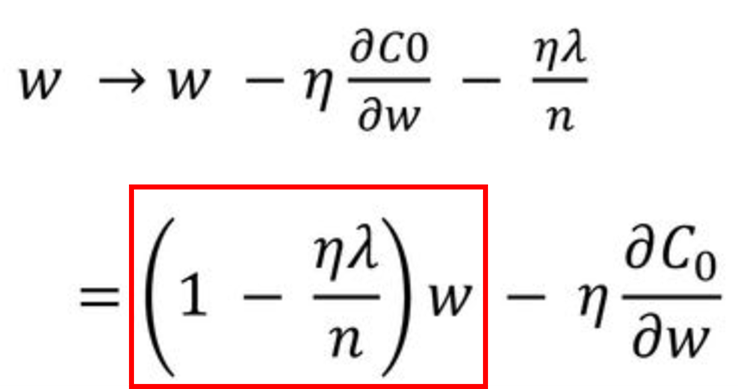
L1과 L2 규제에 대한 Loss Function의 최적해 위치는 아래 그림과 같이 표현될 수 있습니다.
아래 Loss Function의 Space에서 L1, L2의 규제 영역을 두어, 실제 최적값에 대한 bias에 손해를 보더라도 variance를 낮춰 Overfitting 발생을 낮추는 것이라 이해할 수 있습니다.
L1, L2 Loss에서 λ(람다) 값이 커질수록 아래의 규제 영역 크기가 작아지게 되어 bias는 더 커지고 variance는 줄어들게 (underfitting 가능성이 커짐)되며, L1, L2 Regularization을 추가한 Loss Function의 최적값은 규제 영역 내에서 Global Optimum과 제일 가까운 지점이라고 볼 수 있습니다.
아래 그림에서 L1의 경우 θ1의 값이 0인 것을 볼 수 있는데, 이를 통해 특정 변수(Feature)를 삭제할 수 있다는 것을 알 수 있습니다.
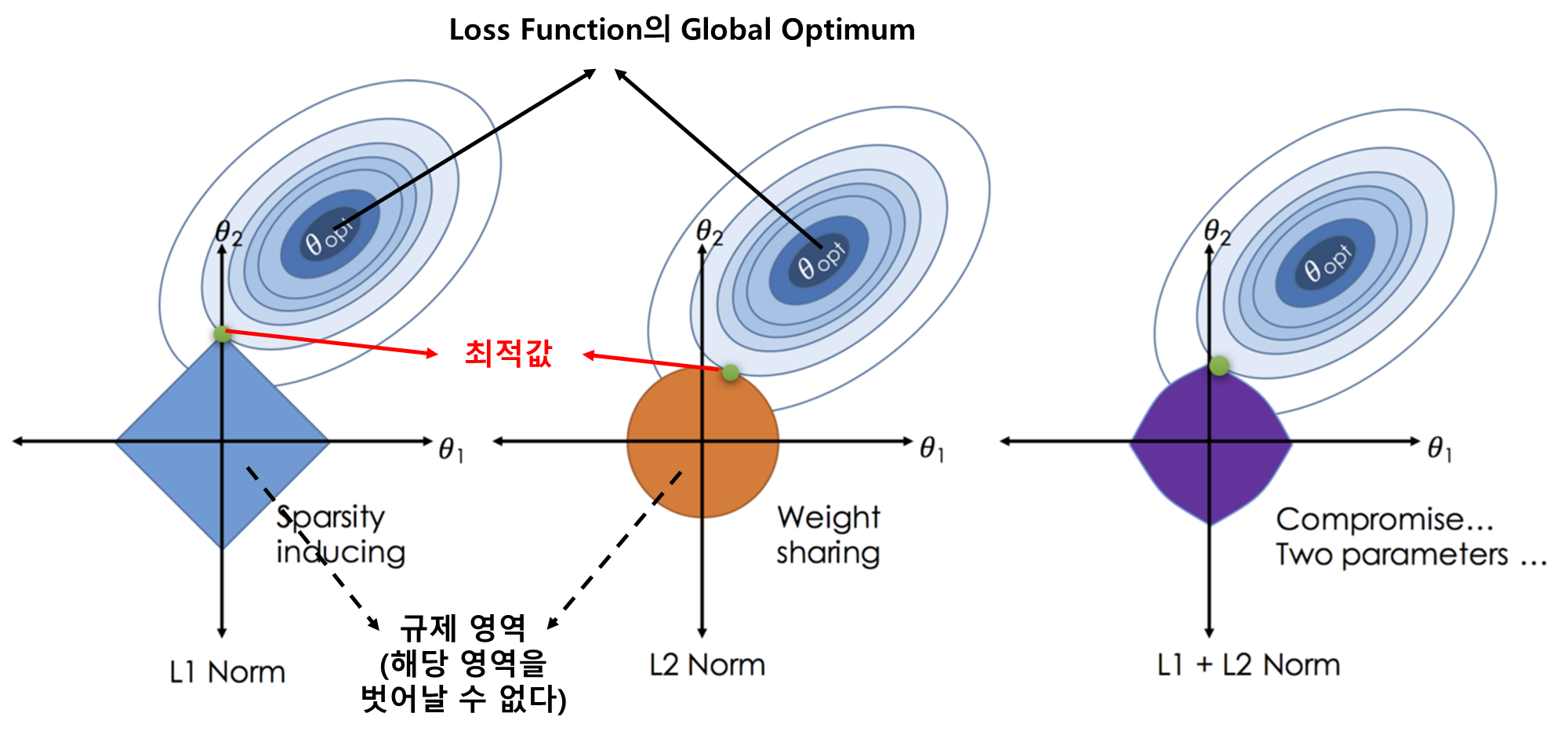
L1과 L2 Regularization을 모두 사용하는 것을 Elastic Net이라고 합니다.
'개발 공부 > ML&DL' 카테고리의 다른 글
| [차원 축소] Kernel-PCA (0) | 2020.03.02 |
|---|---|
| [차원축소] Python 및 사이킷런을 이용한 PCA (1) | 2020.02.23 |
| [차원 축소] 주성분 분석 (PCA, Principal Component Analysis) (0) | 2020.02.09 |
| [차원 축소] 차원 축소 개요 (1) | 2020.01.27 |




댓글