1. Kernel-PCA
1.1 Kernel 기법
PCA, SVM 등에서 사용되는 커널(kernel) 기법은 비선형 함수인 커널함수를 이용하여 비선형 데이터를 고차원 공간으로 매핑하는 기술입니다.
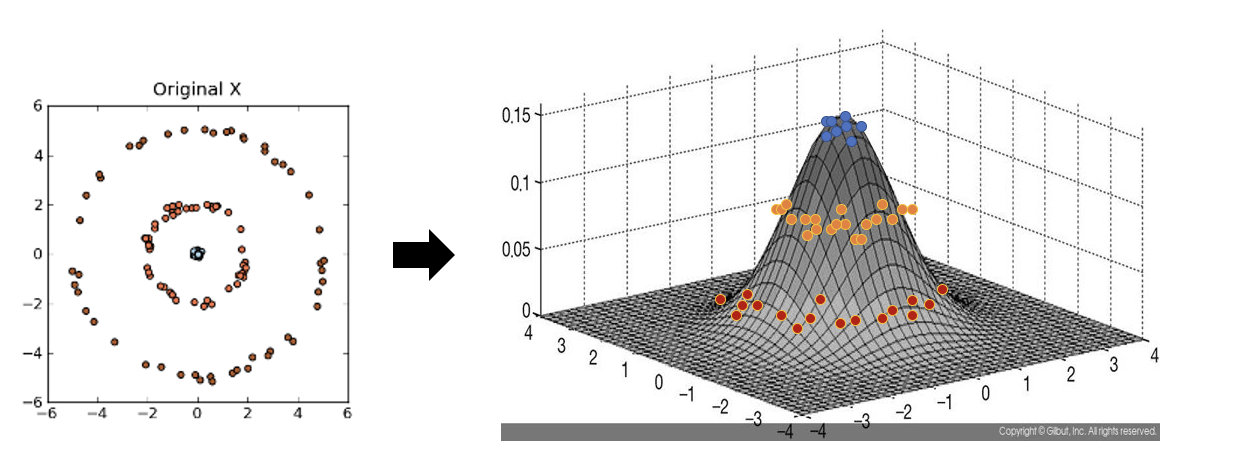
아래 좌측의 데이터 분포를 보면 어떠한 방향으로의 선형변환으로도 데이터 분포를 잘 분류할 수 없을 것 입니다.
그러나 이를 커널함수를 이용해 고차원 공간으로 매핑하여 PCA를 수행한다면 데이터 분포를 분류할 수 있는 결정 공간을 찾을 수 있게 됩니다.
m차원을 n차원으로 매핑하는 매핑함수 $\Phi$에 대해 커널 $K$는 다음과 같이 정의할 수 있습니다.
$$K(x_1, x_2) = {\Phi (x_1)}^T \Phi (x_2)$$
매핑함수 $\Phi$는 선형변환 함수이며, 표준행렬 $A$에 대해 $\Phi (x) = Ax$ 로 표현할 수 있습니다.
따라서 커널 $K$는 다음과 같이 표현 가능합니다.
$$K(x_1, x_2) = {x_1}^T A^T A x_2$$
위의 결과에 의해 $K$의 결과는 스칼라 값을 가지게 됩니다. ${x_1}^T : (1 \times m), A^T : (m \times n), A : (n \times m), x_1 : (m \times 1)$
그리고 Mercer's Theorm에 의해 $K$의 값은 $K(x_1, x_2) = K(x_2, x_1)$을 만족하며 0 이상의 값을 갖는 대칭행렬이어야 합니다.
1.2 Kernel 종류
위의 조건을 만족하면서 흔히 사용되는 커널함수의 종류는 다음과 같습니다.
- Gaussian (RBF) Kernel : $K(x_1, x_2) = exp( {{{\parallel x_1 - x_2 \parallel}^2} \over {2 \sigma^2}} ), \sigma \ne 0$
- Polynomial Kernel : $K(x_1, x_2) = {({x_1}^T x_2 + c)}^d, c > 0$
- Sigmoid Kernel : $K(x_1, x_2) = tanh(a({x_1}^T x_2) + b), a, b \ge 0$
- Linear Kernel : $K(x_1, x_2) = {x_1}^Tx_2$
참고 도서 :
Hands-On Machine Learning with Scikit-Learn & TensorFlow, 한빛미디어
'개발 공부 > ML&DL' 카테고리의 다른 글
| [최적화] 가중치 규제 L1, L2 Regularization의 의미, 차이점 (Lasso, Ridge) (3) | 2022.06.05 |
|---|---|
| [차원축소] Python 및 사이킷런을 이용한 PCA (1) | 2020.02.23 |
| [차원 축소] 주성분 분석 (PCA, Principal Component Analysis) (0) | 2020.02.09 |
| [차원 축소] 차원 축소 개요 (1) | 2020.01.27 |




댓글